원본 : https://catlikecoding.com/unity/tutorials/cube-sphere/
Cube Sphere, a Unity C# Tutorial
A Unity C# scripting tutorial in which we'll turn a cube into a sphere, then improve it with math.
catlikecoding.com
참고 : 이 글은 어디까지나 번역기를 이용해서 최대한 읽기 좋도록 노력해본 것 입니다. 수정을 원한다면 댓글 부탁드립니다.
Cube Sphere
Better Roundness
- 큐브를 구체로 바꿉니다.
- Unity에서 매핑을 시각화 합니다.
- 비판적으로 전환을 바라봅니다.
- 수학을 사용하여 더 나은 접근 방식을 제안합니다.
이 튜토리얼 에서는 큐브를 기반으로 구형 메쉬를 만든 다음 이를 향상시키기 위해 수학적 추론을 사용합니다.
이 자습서는 Rounded Cube를 따릅니다. 해당 자습서는 유니티 5.0.1 이상을 위해 만들어졌습니다.

1. 둥근 큐브 수정
아마도 둥근 큐브로 완벽한 구를 만들 수 있다는 것을 눈치 챘을 것 입니다. 그것이 3차원 모두에서 같은 크기인지 확인하고 둥근 정도를 절반 크기로 설정하십시오.
원하는 모든 것이 구형이라면 둥근 큐브가 제공하는 유연성은 그저 방해가됩니다. 이제 별도로 구성 요소를 만들어 보겟습니다. RoundedCube 스크립트를 복제하고 이름을 CubeShpere어로 바꿉니다. 그런 다음 세 가지 크기를 단일 크기로 변경하고 필요 없는 필드를 제거하십시오.
public class CubeSphere : MonoBehaviour {
public int gridSize;
// No more roundness.
private Mesh mesh;
private Vector3[] vertices;
private Vector3[] normals;
private Color32[] cubeUV;
…
private void Generate () {
GetComponent<MeshFilter>().mesh = mesh = new Mesh();
mesh.name = "Procedural Sphere";
CreateVertices();
CreateTriangles();
CreateColliders();
}
…
}세 개의 필드를 어떻게 대체합니까?
가장 편리한 방법은 편집기를 이용하여 변수 이름을 리팩터링 하는 것 입니다. 이렇게하면 모든 참조가 일므이 바뀌어도 됩니다. 먼저 xSize의 이름을 gridSize로 바꾼 다음 ySize와 zSize에 대해 동일 작업을 수행하세요. 또는 여러개의 검색을 수행하고 작업을 교체하십시오.
gridSize + gridSize 형식의 코드 조각이 나오게 될 것 입니다. 표현을 다시 쓰면서 이것들을 통합할 수 는 있겠지만 그럴 필요가 전혀 없습니다.
roundness 필드를 제거하면 일부 장소에서 계속 사용되므로 오류가 발생합니다. 먼저 충졸자 생성에 대해 살펴 보겠습니다.
둥근 큐브를 나타 내기 위해 여러 상자와 캡슐 콜라이더가 필요했지만 구체에는 단일 구체 콜라이더만 있으면 됩니다. 즉, AddBopxCollider()및 AddCapsuleCollider()를 삭제하고 CreateColliders 단일 코드 행으로 줄일 수 있음을 의미합니다.
private void CreateColliders () {
gameObject.AddComponent<SphereCollider>();
}다음은 roundness에 의존했던 정점의 위치입니다.
모서리 내부에서 원래 큐브의 어딘가를 가리키는 벡터를 정규화하여 둥근 큐브의 모서리를 형성했습니다. 구체로 바뀌면 다른 일이 퇴보하는 것 처럼 우리가 해야할 일 입니다.
우리의 영역이 지역의 원점에 집중되어 있다면 편리 할 것 입니다. 우리는 그리드와 둥근 큐브를 사용하여 이 작업을 수행하지 않았습니다. 그러나 이 경우에는 구체의 생성이 더 간단해지므로 중심에 둡니다.
단위 구 반경이 1인 구를 만들려면 원점을 중심으로 한 정육면체의 정점이 정규화해야합니다. 그 큐브가 정확하게 구를 포함하려면 가장자리 길이가 2가 되어야 합니다.

SetVertex 원시 좌표를 그리드 크기로 나누고 두배로 한 다음 한 점을 빼서 이 큐브의 정점을 만들 수 있습니다.
public float radius = 1;
private void SetVertex (int i, int x, int y, int z) {
Vector3 v = new Vector3(x, y, z) * 2f / gridSize - Vector3.one;
normals[i] = v.normalized;
vertices[i] = normals[i];
cubeUV[i] = new Color32((byte)x, (byte)y, (byte)z, 0);
}단위 구가 생기지만 다른 반경을 원할 수 있습니다. 그럼 구성 가능하도록 합시다.
public float radius = 1f;
private void SetVertex (int i, int x, int y, int z) {
Vector3 v = new Vector3(x, y, z) * 2f / gridSize - Vector3.one;
normals[i] = v.normalized;
vertices[i] = normals[i] * radius;
cubeUV[i] = new Color32((byte)x, (byte)y, (byte)z, 0);
}이제는 모든 오류가 사라져야 하며, 처음부터 둥근 큐브 개체의 구성 요소를 대체하거나 큐브 구체 개체를 장면에 넣을 수 있습니다.


2. 매핑 조사
우리는 구형 메쉬를 만드는 방법을 가지고 있지만 그것들은 얼마나 좋을까요? 여러 시점에서 구를 살펴봅시다. 그리드가 균등한가요?




그리드 셀의 크기는 꽤 다양합니다. 가장 큰 셀은 큐브 얼굴의 가운데에서 옵니다. 그들은 큐브 모서리에서 나온 가장 작은 셀의 대략 4배에 이릅니다.
이것이 왜 그렇게 보이는지 알아보려면 사각형에서 원으로 매핑을 시각화합니다. 우리는 원보다 더 쉽게 작업할 수 있기 때문에 원을 사용할 것 입니다. 문제의 한 조각 일 뿐입니다.
Gizmos를 사용하여 Unity에서 시각화를 만들 수 있습니다. OnDrawGizmosSelected 메소드와 함께 맞춤 구성 요소를 사용합니다. 그것은 OnDrawGizmos기즈모가 객체가 선택되었을 때에 만 드로잉 된다는 점을 제외하면 작동합니다. 그렇게 하면 장면에 시각화 개체를 추가할 수 있습니다. 이 개체는 선택하지 않으면 보이지 않습니다.
using UnityEngine;
public class CircleGizmo : MonoBehaviour {
private void OnDrawGizmosSelected () {
}
}우리는 검은 영역으로 정사각형 가장자리에 꼭지점을 표시하고, 우리가 원하는 해상도로 시작합니다. 위쪽과 아래쪽 가장자리부터 시작합니다.
public int resolution = 10;
private void OnDrawGizmosSelected () {
float step = 2f / resolution;
for (int i = 0; i <= resolution; i++) {
ShowPoint(i * step - 1f, -1f);
ShowPoint(i * step - 1f, 1f);
}
}
private void ShowPoint (float x, float y) {
Vector2 square = new Vector2(x, y);
Gizmos.color = Color.black;
Gizmos.DrawSphere(square, 0.025f);
}

왼쪽과 오른쪽 가장자리를 채워 사각형을 완성하십시오. 코너가 이미 표시되어 있으므로 지금 건너 뛸 수 있습니다.
private void OnDrawGizmosSelected () {
float step = 2f / resolution;
for (int i = 0; i <= resolution; i++) {
ShowPoint(i * step - 1f, -1f);
ShowPoint(i * step - 1f, 1f);
}
for (int i = 1; i < resolution; i++) {
ShowPoint(-1f, i * step - 1f);
ShowPoint(1f, i * step - 1f);
}
}
다음으로 각 점에 대해 흰색 원을 사용하여 해당 원 버텍스를 표시합니다. 그런 다음이 두 정점 사이의 관계를 노란색 선으로 표시합니다. 그리고 마지막 동그라미 꼭지점에서 중심까지의 회색 선을 잇습니다.
private void ShowPoint (float x, float y) {
Vector2 square = new Vector2(x, y);
Vector2 circle = square.normalized;
Gizmos.color = Color.black;
Gizmos.DrawSphere(square, 0.025f);
Gizmos.color = Color.white;
Gizmos.DrawSphere(circle, 0.025f);
Gizmos.color = Color.yellow;
Gizmos.DrawLine(square, circle);
Gizmos.color = Color.gray;
Gizmos.DrawLine(circle, Vector2.zero);
}
이제 매핑이 어떻게 작동하는지 볼 수 있습니다. 정규화는 정점을 단위 원에 도달할 때 까지 가운데로 곧 바로 가져옵니다. 정사각형의 모서리에 더 가깝게 위치한 정점은 주축에 더 가까운 저점보다 많이 끌어당깁니다. 사실, 주축에 정확히 놓여있는 정점은 전혀 이동하지 않으며, 댁가선에 정확하게 놓이는 정점은 √2−1 만큼 이동합니다.
움직이는 모든 포인트가 똑같은 포인트쪽으로 똑바로 당겨지기 때문에, 그들은 더 가깝게 끝납니다. 그렇기 때문에 대각선에 닿는 셀이 가장 작습니다.
3. 수학과 놀아 봅시다
(뭐 이딴.. 읽기 전 참고 : 수식이 어려워 보인다고 훑듯이 넘어가지 마세요. 설명을 읽고 잠시 멈춰보면 왜 이 수식을 보여주는가 알 수 있습니다.)
지금까지 우리는 셀이 다른 크기로 끝나는 이유를 알아보았습니다. 그것에 대해 뭔가 할 수 있을까요? 어쩌면 보다 균일한 한 셀을 생성하는 다른 매핑이 있을 수 있습니다. 그렇다면 그러한 매핑을 어떻게 찾을 수 있을까요?
이 문젠 실제로 수학적 문제이므로, 우리의 현재 매핑을 더 공식적으로 기술 해 보겠습니다. 다시 한 번 우리는 처음부터 원에 대해서만 관심을 가집니다. 나중에 구체화 할 수 있다고 가정합니다.
따라서 우리는 정사각형의 점을 원의 점으로 매핑할 것 입니다. 벡터를 사용하여 점을 설명 할 때 실제로 벡터를 다른 벡터에 매핑합니다.

특히, 우리 원은 모서리 길이 2의 정사각형을 나타내는 단위 원입니다. 그래서 우리의 지도는 단순히 벡터 Vs의 정규화된 버전입니다.

벡터를 정규화한 것은 벡터의 길이로 나눕니다.
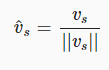
2D 벡터의 길이는 어떻게 구할까요? 이것은 두 좌표로 구성됩니다.

이 좌표는 피타고라스의 정리를 적용 할 수 있는 직각 삼각형을 정의합니다.


벡터의 길이는 단순히 이 수식의 결과의 제곱근입니다.

이제 가장 명확한 형식으로 매핑을 작성할 수 있습니다.

좋습니다. 하지만 'Vc'가 단위 원에 점을 정의한다는 것을 실제로 증명할 수 있을까요? 그렇게하기 위해서는 길이가 1이어야 합니다. 그래서 우리는 실질적으로 참인지 증명해내야 합니다.

이 수식은 잘 작동하지 않으므로 모든 것을 정사각형으로 만들어 봅시다.
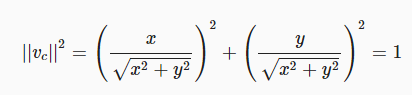
수식을 단순화하는 것이 가능합니다

최종 표현식의 분자와 분모가 동일하므로 결과는 1이어야 합니다. 즉, x^2 + y^2 결과는 정의되지 않습니다. 그러나 사각형 모서리에있는 점을 입력으로 사용하기 때문에 좌표 중 하나 또는 둘 모두가 1또는 -1로 되어 x^2 + y^2 >= 1이 보장됩니다. 그래서 우리는 정의되지 않은 결과를 얻지 못할 것 입니다.
이 증명이 유용했나요? 우리 사각형의 각 점에 대해 1을 산출하는 수식이 있음을 보여줍니다. 이 수식은 사각형에서 단위 원으로 매핑에 해당됩니다.
같은 것을 하는 다른 수식을 찾을 수 있나요? 그렇다면 다른 매핑이 있어야합니다! 그래서 과정을 뒤집어 보려합니다. 우리 사각형의 모든 점에 대해 1을 산출하는 수식을 제안해주세요.
우리가 가능한 한 간단한게 유지하려고 한다면 그러한 기능은 어떻게 생겼을까요? 좌표 중 적어도 하나는 항상 -1또는 1입니다. 따라서 두 좌표를 모두 정사각형으로 만들려면 최소 하나의 단일 좌표를 얻습니다. 또는 1 - x^2 및 1 - y^2를 사용하여 좌표를 0으로 만들 수 있습니다. 이들 중 적어도 하나가 항상 0이므로, 이들을 곱하면 0이 됩니다. 이것은 우리에게 공식을 제공합니다.

왜 덧셈 대신 1을 빼나요?
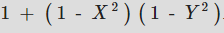
해당 수식 또한 유효합니다. 이 공식은 원점에서 제로를 산출하고 원점으로부터 더 멀리 떨어진 지점에 대해 더 큰 결과를 산출하기 때문에 빼기가 덧셈보다 더 직관적입니다. 또한 우리가 다시 쓸 때 1을 제거할 수 있어서 편리합니다.
이 수식은 더 간단한 형식으로 다시 작성할 수 있습니다.

어떻게 다시 작성할수 있을까요?
다음 두가지 단계를 따릅니다.
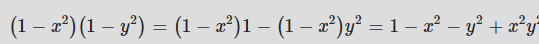
최종 결과는 1을 뺀 것입니다. (무슨 소리냐면, 맨 오른쪽 보면 1 - ... 이 생기는데 이 것은 위의 수식의 1-랑 별개이므로 1 - (1 - ...)가 됩니다. 따라서 1은 빼지면서 사라진거에요. 그래서 보면 이 접음글 바로 전 수식에선 1이 없습니다.
이제 Vc의 사각형 길이를 정의하는 새로운 방법이 생겼습니다.

이 방정식의 오른쪽을 다시 배열하여 a+b 형식으로 합니다. x^2 및 y^2은 분명하지만 (x^2)(y^2)로 무엇을 할 까요? 상황을 최대한 대칭으로 유지하는 것이 중요하므로 똑같이 분리하세요.

우리는 이것을 두개의 좌표로 나눌 수 있습니다.

우리는 그것을 다르게 분할 할 수 있찌만, 이 방버은 원에서 점의 가능한 최상의 분포를 만듭니다. 이제 우리는 최종 벡터로부터 단지 제곱근입니다.
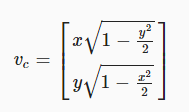
-> 각 좌표에 해당하는 것을 제곱근의 결과로 뺴오면서 사실상 곱하면 같은 수식이 되는 구조입니다. 자세한건 아래 접음글
어떻게 재작성 했나요?
Xc에 대한 것 입니다.
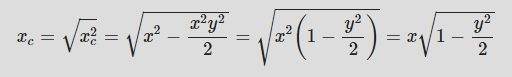
우리가 방금 발견 한 벡터는 사각형에서 원으로의 새로운 매핑을 제공합니다. 바로 시도 해보죠!
Vector2 circle;
circle.x = square.x * Mathf.Sqrt(1f - square.y * square.y * 0.5f);
circle.y = square.y * Mathf.Sqrt(1f - square.x * square.x * 0.5f);
이 매핑은 점을 대가선에서 축 방향으로 밀어냅니다. 그들은 이제 축 근처에서 가장 가깝습니다. 다행스럽게도 인접한 점 사이의 거리는 첫 번째 접근 방식보다 더 균일하므로 개선 되었습니다.
4. 매핑 조정
우리는 사각형에서 원까지 새로운 매핑을 가지고 있습니다. 그러나 큐브에서 구체로 가는 것은 어떨까요? 같은 접근법을 사용할 수 있을까요? 할 수 있습니다. 하지만, 이미 가지고있는 두 가지 좌표와 마찬가지로 세 번째 좌표를 통합해야합니다. 그렇게하면 단위 구의 점을 가리키는 벡터의 사각형 길이를 얻을 수 있습니다.

사실, 이것은 어떤 양의 좌표에서도 작동합니다. 그래서 우리는 모든 하이퍼 큐브에서 동일한 차원의 어떤 하이퍼 피어로 매핑할 수 있습니다. 확장 된 수식은 더 복잡해집니다.

어떻게 다시 작성할까요?
우린 이미 두 좌표를 다루는 방법을 알고 있습니다.
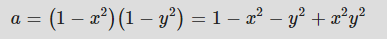
이로 인해 다음과 같은 중간 단계가 발생합니다.
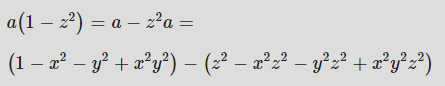
최종 결과는 1을 뺀 것입니다. (2차원에서도 똑같이 마지막에 남은 1이 1-과 만나 사라진 것 입니다.)
3차원에 대한 수식에는 새로운 형태가 있습니다. (x^2)(y^2)(z^2) 세 좌표 모두에 연결되어 있습니다. 이전과 마찬가지로 최종 벡터의 좌표 사이에서 균등하게 분할합니다. 우리는 더 복잡한 공식으로 끝나지만 개념은 동일하게 유지됩니다. 여기에 X^2o가 있습니다. 다른 것은 유사합니다.

다시 한번 최종 매핑은 단지 제곱근입니다.

SetVertex에 실질적으로 어떻게 적용되는지 봅시다!
private void SetVertex (int i, int x, int y, int z) {
Vector3 v = new Vector3(x, y, z) * 2f / gridSize - Vector3.one;
float x2 = v.x * v.x;
float y2 = v.y * v.y;
float z2 = v.z * v.z;
Vector3 s;
s.x = v.x * Mathf.Sqrt(1f - y2 / 2f - z2 / 2f + y2 * z2 / 3f);
s.y = v.y * Mathf.Sqrt(1f - x2 / 2f - z2 / 2f + x2 * z2 / 3f);
s.z = v.z * Mathf.Sqrt(1f - x2 / 2f - y2 / 2f + x2 * y2 / 3f);
normals[i] = s;
vertices[i] = normals[i] * radius;
cubeUV[i] = new Color32((byte)x, (byte)y, (byte)z, 0);
}



그리드 셀은 여전히 대각선에 가까이 갈수록 왜곡됩니다. 그 주위에는 방법이 없습니다. 그러나 이 새로운 매핑은 정규화 방법보다 훨씬 더 균일 한 크기의 셀을 생성합니다. 축과 큐브 모서리에 있는 셀은 이제 거의 동일한 크기로 나타납니다. 우리가 시작한 것보다 훨씬 좋습니다! 가장 큰 셀은 이제 큐브의 가장자리를 따르는 셀입니다. 부숴 지곤 했지만 지금은 뻗어 있습니다.
어떻게 그런 수학을 생각할 수 있을까요?
논리적인 순서로 여기에 제시되지만 일반적으로 이 항목을 알아내는 것은 훨씬 더 불규칙한 경로를 취합니다. 명확한 논리적 경로를 따르면 기회가 주어지면 좋지만 직감은 종종 실험을 통해서만옵니다. 그리고 그 전에 다른 사람들이 이미 알아 낸 것을 조사하십시오.
인터넷은 많은 지식을 보유하고 있습니다. 이 경우 큐브 스피어 매핑은 Philip Nowell이 자신의 블로그에서 설명했습니다. 매핑의 직감은 Mathematics Stack Exchange 질문에 대한 답에서 나옵니다.
이 멋진 구체에 좋은 짜냄을 주는 느낌이 들었다면, Mesh Deformation 자습서로 이동할 수 있습니다.
'Unity > 3D' 카테고리의 다른 글
| Unity3D - Animator와 SkinnedMeshRenderer에 대한 오해가능 요소 (0) | 2020.10.06 |
|---|---|
| Unity C# Tutorials - Mesh Deformation(Making a Stress Ball) 번역본 (0) | 2019.07.12 |
| Unity C# Tutorials - Rounded Cube(Building in 3D) 번역본 (1) | 2019.07.06 |
| Unity C# Tutorials - Procedural Grid (Programming Form) 번역본 (0) | 2019.06.28 |



